Transformations and SymmetrySymmetry Groups and Wallpapers
Some shapes have more than one symmetry – let’s have a look at the








You have already shown above that a square has
It also has rotational symmetry by
And finally, we can think about “doing nothing” as another special kind of symmetry – because the result is (obviously) the same as before. This is sometimes called the identity.
In total, we have found
Now we can actually start doing some arithmetic with these symmetries. For example, we can add two symmetries to get new ones:






Whenever you add two symmetries of a square, you get a new one. Here is a “symmetry calculator” where you can try it yourself:
Spend some time playing around with the symmetry calculator, and try to find any patterns. Can you complete these observations?
- Adding two rotations will always give
(or the identity). - Adding two reflections will always give
(or the identity). - Adding the same two symmetries in the opposite order
result. - Adding the identity
.
You might have realised already that adding symmetries is actually very similar to adding integers:
- Adding two symmetries/integers always gives another symmetry/integer:
+ = 12 + 7 = 19 - Adding symmetries/integers is
associative :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Every symmetry/integer has an inverse, another symmetry/integer which, when added, gives the identity:
+ = 4 + –4 = 0
In mathematics, any collection that has these properties is called a
In this example, we started with the eight symmetries of the square. In fact, every geometric shape has its own symmetry group. They all have different elements, but they always satisfy the three rules above.
Groups appear everywhere in mathematics. The elements can be numbers or symmetries, but also polynomials, permutations, matrices, functions … anything that obeys the three rules. The key idea of group theory is that we are not interested in the individual elements, just in how they interact with each other.
For example, the symmetry groups of different molecules can help scientists predict and explain the properties of the corresponding materials.
Groups can also be used to analyse the winning strategy in board games, the behaviour of viruses in medicine, different harmonies in music, and many other concepts…
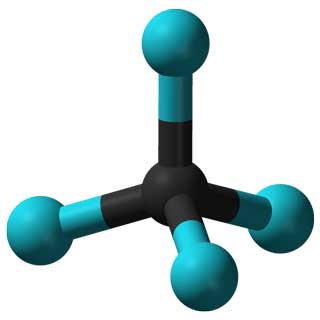
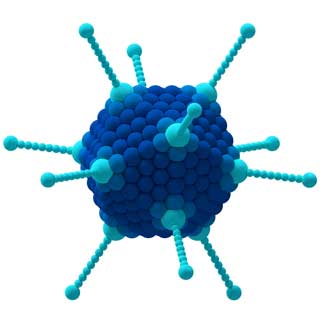
The properties of the CCl4 molecule (left) and the Adenovirus (right) are determined by their symmetries.
Wallpaper Groups
In the previous sections we saw two different kinds of symmetry corresponding to two different transformations: rotations and reflections. But there is also a symmetry for the third kind of rigid transformation:


Hexagonal honyecomb


Ceramic wall tiling
In addition to reflectional, rotational and translational symmetry, there even is a fourth kind:


A pattern can have more than one type of symmetry. And just like for squares, we can find the
These groups don’t tell you much about how the pattern looks like (e.g. its colours and shapes), just how it is repeated. Multiple different patterns can have the same symmetry group – as long are arranged and repeated in the same way.


These two patterns have the same symmetries, even though they look very different. But symmetries are not about colours, or superficial shapes.


These two patterns also have the same symmetries – even though they look more similar to the corresponding patterns on the left, than to each other.
It turns out that, while there are infinitely many possible patterns, they all have one of just 17 different symmetry groups. These are called the Wallpaper Groups. Every wallpaper group is defined by a combination of translations, rotations, reflections and glide reflections. Can you see the

Group 1 – P1
Only translations

Group 2 – P2
Rotations of order 2, translations

Group 3 – P3
Rotations of order 3 (120°), translations

Group 4 – P4
Four rotations of order 2 (180°), translations

Group 5 – P6
Rotations of order 2, 3 and 6 (60°), translations

Group 6 – PM
Parallel axes of reflection, translations

Group 7 – PMM
Perpendicular reflections, rotations of order 2, translations

Group 8 – P4M
Rotations (ord 2 + 4), reflections, glide reflections, translations

Group 9 – P6M
Rotations (ord 2 + 6), reflections, glide reflections, translations

Group 10 – P3M1
Rotations of order 3, reflections, glide reflections, translations

Group 11 – P31M
Rotations of order 3, reflections, glide reflections, translations

Group 12 – P4G
Rotations (ord 2 + 4), reflections, glide reflections, translations

Group 13 – CMM
Perpendicular reflections, rotations of order 2, translations

Group 14 – PMG
Reflections, glide reflections, rotations of order 2, translations

Group 15 – PG
Parallel glide reflections, translations

Group 16 – CM
Reflections, glide reflections, translations

Group 17 – PGG
Perpendicular glide reflections, rotations of order 2, translations
Unfortunately there is no simple reason why there are 17 of these groups, and proving it requires more advanced mathematics. Instead, you can try drawing your own repeated patterns for each of the 17 wallpaper groups:
Examples of other students’ drawings



The wallpaper groups were all about flat, two-dimensional patterns. We can do something similar for three-dimensional patterns: these are called crystallographic groups, and there are 219 of them!
In addition to translations, reflections, rotations, and glide reflections, these groups include symmetries like glide planes and screw axes (think about the motion when unscrewing a bottle).
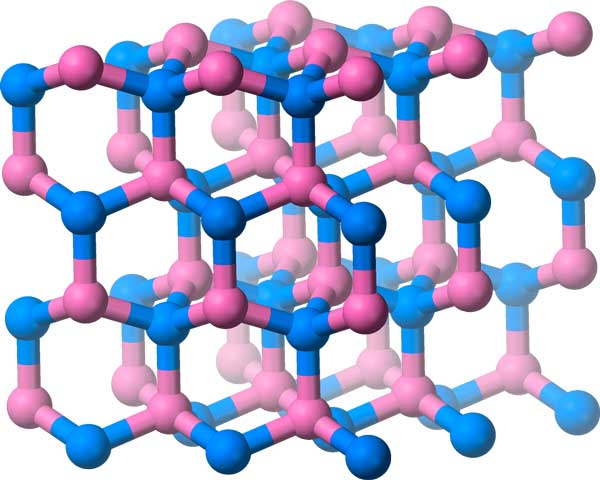
Boron-Nitride has its molecules arranged in this crystal lattice, which has a three-dimensional symmetry group.