FractalsIntroduction
When looking around nature, you might have noticed intricate plants like these:


This Fern consists of many small leaves that branch off a larger one.


This Romanesco broccoli consists of smaller
Initially, these appear like highly complex shapes – but when you look closer, you might notice that they both follow a relatively simple pattern: all the individual parts of the plants look exactly the same as the entire plant, just smaller. The same pattern is repeated over and over again, at smaller scales.
In mathematics, we call this property self-similarity, and shapes that have it are called
To create our own fractals, we have to start with a simple pattern and then repeat it over and over again, at smaller scales.
One of the simplest patterns might be a line segment, with two more segments branching off one end. If we repeat this pattern, both of these blue segments will also have two more branches at their ends.
You can move the blue dots to change the length and angle of all of the branches. Then increase the number of iterations using
Depending on the position of the branches, you can make completely different patterns – looking like the above, a , or . What else can you find?
Another famous fractal is the
Notice how the final shape is made up of three identical copies of itself, and each of these is made up of even smaller copies of the entire triangle! You could keep zooming into the triangle forever, and the patterns and shapes will always continue repeating.
The plants at the beginning of this chapter look just like fractals, but it is clearly impossible to create true fractals in real-life. If we keep repeating the same pattern over and over again, smaller and smaller, we would eventually get to cells, molecules or atoms which can no longer be divided.
However, using mathematics, we can think about the properties that real fractals “would” have – and these are very surprising…
Fractal Dimensions
First, let’s think about the dimension of fractals. A line has dimension
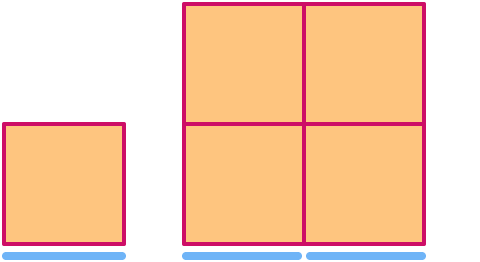
A square has dimension
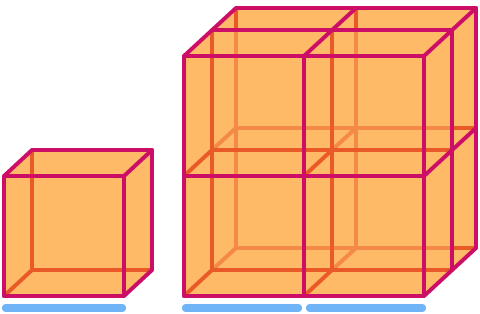
A cube has dimension
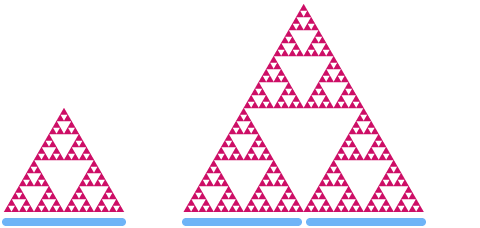
Now let’s have a look at the Sierpinski triangle. If we scale it by a factor of 2, you can see that it’s “area” increases by a factor of
Let’s say that d is the dimension of the Sierpinski triangle. Using the same pattern as above, we get
But wait … how can something have a dimension that is not an integer? It seems impossible, but this is just one of the weird properties of fractals. In fact, this is what gives fractals their name: they have a fractional dimension.
With every iteration, we remove some of the area of the Sierpinski triangle. If we could do this infinitely many times, there would actually be no area left: that’s why the Sierpinski triangle is something in-between a two-dimensional area, and a one-dimensional line.
While many fractals are self-similar, a better definition is that fractals are shapes which have a non-integer dimension.
The Koch Snowflake
There are many shapes in nature that look like fractals. We’ve already seen some plants at the beginning of this chapter. Other great examples are snowflakes and ice crystals:
To create our own fractal snowflake, we once again have to find a simple procedure we can apply over and over again.
Like the Sierpinski triangle, let’s start with a single, equilateral triangle. However, rather than removing smaller triangles at every step, we add smaller triangles along the edge. The side-length of every triangle is
The resulting shape is called the
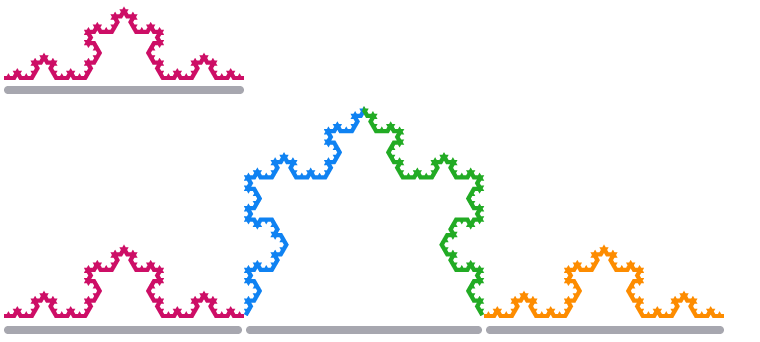
When we scale one edge segment of the Koch Snowflake by a factor of 3, its length
Using the same relationship between dimensions and scale factors as above, we get the equation
Area
Creating the Koch snowflakes is almost like a




After the first iteration, the number of new triangles added increases by a factor of
Let’s say that the
Using the formula for the sum of infinite
Perimeter
We can also try to calculate the perimeter of the Koch snowflake. As we have already seen before, the length of the perimeter changes by a factor of
This means that, once again, we have a geometric series – but in this case, it

If this seems counterintuitive, just remember that we multiply the perimeter by
It is almost unthinkable that you can have a shape with a finite area and also an infinite circumference – but this is just one of the many unexpected properties of fractals.
Can you come up with any other ways to create your own fractals?
Menger Sponge
Fractals don’t have to be “flat”, like many of the examples above. One of the most famous fractals that look three-dimensional is the Menger sponge, named after the mathematician
We start with a solid cube, and repeatedly drill smaller and smaller holes into its sides. Every new iteration of holes has
A
Now we can try to calculate the dimension d of the Menger sponge just like we did for the Koch snowflake above. In this case we get
If you imagine cutting out more and more holes, infinitely many times, there would be no actual volume left. That’s why the cube is “not quite” three-dimensional!
Fractal Coastlines
One of the key characteristics of all the fractals we’ve seen so far is that you can “zoom in” forever and always find new patterns. Around 1920, the British mathematician
You start with the basic shape of the country, and, as you zoom in, you add river inlets, bays and estuaries, then individual cliffs, rocks, pebbles, and so on:
This is a significant problem when trying to calculate the length of the border of a country – how do you decide how far to zoom in, and which nooks and crannies to include?
One way we could measure the length of Britain’s coastline, for example, is to take a long ruler, walk all the way around its beaches, and then add up all the distances.
If the ruler is
We can just keep going, with smaller and smaller rulers, and each time our result for the length of the coastline would get a bit longer. Just like the Koch Snowflake before, it seems that Britain’s coastline is infinitely long! This is often called the coastline paradox.
A few decades later, the mathematician
The coastline of Britain certainly “looks” fractal, but it is not self-similar, like other fractals we’ve seen before. In order to find its size, we can draw it on a grid and count the number of cells that it intersects with.
Initially, there are 88 intersecting cells. If we scale the coastline by a factor of 2, there are 197 intersecting cells – more than twice as many!
The size of the coastline has increased by a factor of
If we repeat this with larger grids, we’d find that the dimension of Britain’s coastline is actually approximately 1.21. Mandelbrot realised that this fractal dimension is also a measure of the roughness of a shape – a new concept, for which he found important applications in many other areas of mathematics and science.
More Fractals in Nature and Technology
While true fractals can never appear in nature, there are many objects that look almost like fractals. We’ve already seen plants, snowflakes and coastlines, and here are some more examples:
Mountain range in central Asia
Ganges river delta in India
Lightning bolts
Blood vessels in the retina
Grand Canyon in the USA
Clouds
All these objects might appear completely random, but, just like fractals, there is an underlying pattern that determines how they are formed. Mathematics can help us understand the shapes better, and fractals have applications in fields like medicine, biology, geology and meteorology.
Computer-generated fractal terrain
We can also use fractals to create realistic “copies” of nature, for example, as landscapes and textures used in video games or computer-generated movies. The water, mountains and clouds in this image are made entirely by a computer, with the help of fractals!
And we can even reverse this process to compress digital images, to reduce their file size. The first algorithms were developed by Michael Barnsley and Alan Sloan in the 1980s, and new ones are still being researched today.