Polygons and PolyhedraTessellations
Sinaloan Milk Snake skin
Cellular structure of leafs
Basalt columns at Giant’s Causeway in Northern Ireland
Pineapple skin
Shell of a tortoise
Humans have copied many of these natural patterns in art, architecture and technology – from ancient Rome to the present. Here are a few examples:
Greenhouse at the Eden Project in England
Mosaic at Alhambra
Cellular tessellation pavilion in Sydney
Study of Regular Division of the Plane with Reptiles, M. C. Escher
Here you can create your own tessellations using regular polygons. Simply drag new shapes from the sidebar onto the canvas. Which shapes tessellate well? Are there any shapes that don’t tessellate at all? Try to create interesting patterns!
Examples of other students’ tessellations

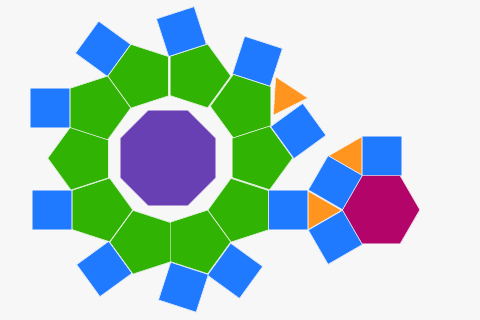
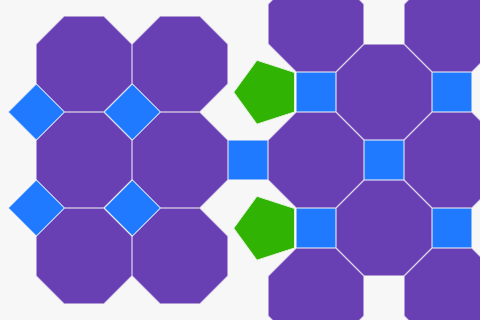
Tessellations from regular polygons
You might have noticed that some
This has to do with the size of their
Triangles
Squares
Pentagons
Hexagons
You can similarly check that, just like pentagons, any regular polygon with 7 or more sides doesn’t tessellate. This means that the only regular polygons that tessellate are triangles, squares and hexagons!
Of course you could combine different kinds of regular polygons in a tessellation, provided that their internal angles can add up to 360°:

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Hexagons and triangles
120° + 120° + 60° + 60° = 360°

Hexagons and triangles
120° + 60° + 60° + 60° + 60° = 360°

Hexagons, squares and triangles
120° + 90° + 90° + 60° = 360°

Octagons and squares
135° + 135° + 90° = 360°

Dodecagons (12-gons) and triangles
150° + 150° + 60° = 360°

Dodecagons, hexagons and squares
150° + 120° + 90° = 360°
Tessellations from irregular polygons
We can also try making tessellations out of
It turns out that you can tessellate not just equilateral triangles, but any triangle! Try moving the vertices in this diagram.
The sum of the internal angles in a triangle is
More surprisingly, any quadrilateral also tessellates! Their internal angle sum is
Pentagons are a bit trickier. We already saw that regular pentagons
Here are three different examples of tessellations with pentagons. They are not regular, but they are perfectly valid 5-sided polygons:
Over time, mathematicians have only found 15 different kinds of tessellations with (convex) pentagons – the most recent of which was discovered in 2015.
Two years later, in 2017, Michaël Rao published a proof that there are no other possibilities, except the 15 that had already been found. Can you make a tessellation using all of them?
Tessellations in Art
Many artists, architects and designers use tessellations in their work. One of the most famous examples is the Dutch artist
“Sky and Water I” (1938)
“Lizard” (1942)
“Lizard, Fish, Bat” (1952)
“Butterfly” (1948)
“Two Fish” (1942)
“Shells and Starfish” (1941)
These artworks often look fun and effortless, but the underlying mathematical principles are the same as before: angles, rotations, translations and polygons. If the maths isn’t right, the tessellation is not going to work!
“Metamorphosis II” by M. C. Escher (1940)
Penrose Tilings
All the tessellations we saw so far have one thing in common: they are periodic. That means they consist of a regular pattern that is repeated again and again. They can continue forever in all directions and they will look the same everywhere.
In the 1970s, the British mathematician and physicist
Move the slider to reveal the underlying structure of this tessellation. Notice how the same patterns appear at various scales: the yellow pentagons, blue stars, purple rhombi and green ‘ships’ appear in their original size, in a slightly larger size and an even larger size. This self-similarity can be used to prove that a Penrose tiling is always non-periodic.
Penrose was exploring tessellations purely for fun, but it turns out that the internal structure of some real materials (like aluminium) follow a similar pattern. The pattern was even used on toilet paper, because the manufacturers noticed that a non-periodic pattern can be rolled up without any bulges.
