Üçgenler ve TrigonometriPisagor Teoremi
Geometride önemli bir noktaya ulaştık – matematikteki en ünlü
Pisagor Teoremi Dik açılı bir üçgende, hipotenüsün (dik açının karşısındaki kenar) uzunluğunun karesi diğer iki kenarın uzunluklarının kareleri toplamına eşittir. Diğer bir deyişle,
Tersi de doğrudur: eğer bir üçgendeki kenarlar a*{sup}2* + b*{sup}2* = c*{sup}2* eşitliğini sağlarsa, bu üçgen

Dik açılar her yerdedir, ve bu nedenle Pisagor Teoremi çok kullanışlıdır.
Burada 6m uzunluğunda duvara yaslanmış bir merdiven görüyorsunuz. Merdivenin alt kısmı duvardan 1m uzaklıkta bulunuyor. Duvara ne kadar ulaşır?
Merdiven, duvar ve yerin bir dik üçgen oluşturduğunu fark edelim. Pisagor Teoremi’ni kullanarak şunu elde ederiz:
Elinizdeki dik üçgenin iki kenarını bildiğinizde, Pisagor Teoremi üçüncü kenarı bulmanıza yardımcı olur.
Pisagor Teoremi’nin Kanıtı
Pisagor Teoremi, Babilliler, Mezopotamyalılar, Hintliler ve Çinliler tarafından biliniyordu – ancak Pisagor düzgün, matematiksel kanıtı yapan ilk kişidir.
Aslında Pisagor Teoremi’ni kanıtlamanın birçok farklı yolu vardır. Burada her birinin farklı strateji kullandığı üç farklı örneği görebilirsiniz:
Yeniden Düzenleme
Sağdaki şekle bakın. Şekildeki karenin bir kenarı a + b uzunluğundadır, dört dik üçgen ve aynı zamanda alanı
Şimdi karedeki üçgenleri yeniden düzenleyelim. Sonuç yine dik açılı dört üçgen ve aynı zamanda alanları
Kırmızı bölgenin alanını, yerdeğiştirmeden önce ve sonra olarak karşılaştırdığımızda şunu görürüz:
Bu
Cebir
Öncekiyle aynı şekli yanda görüyoruz, ama bu kez Pisagor Teoremi’ni yeniden düzenleme yerine cebir kullanarak kanıtlayacağız.
Büyük karenin bir kenarı
Her birinin alanı
Eğer tüm bu bilgileri kullanacak olursak, şuna ulaşırız
Ve bir kez daha Pisagor Teoremi’ni kanıtladık.
Benzer Üçgenler
Burada başka bir dik üçgen görüyorsunuz. Eğer birinin yüksekliğini çizersek, iki farklı daha küçük dik üçgene ayrılır. Bu aynı zamanda hipotenüsü c de, x ve y olarak adlandıracağımız iki küçük parçaya böler.
Şimdi aralarındaki ilişkiyi daha açık görmek için bu iki üçgeni ayıralım…
Küçük üçgenlerin ikisi de orijinal üçgenle ortak bir açıyı paylaşırlar. Ayrıca hepsi bir dik açıya sahiptir. AA şartından, üç üçgenin de
Şimdi zaten benzer çokgenler hakkında bildiğimiz denklemleri kullanabiliriz:
Ancak c = x + y olduğunu hatırlayın. Böylece
Bir kez daha Pisagor Teoremi’ni kanıtladık!
Pisagor’un hayatıyla ilgili çok az şey bilinir ve çalışmalarının orijinal hali günümüze kadar ulaşmamıştır. Pisagor, “Sayı ibadeti” denilebilecek bir çeşit dini bir kült , Pisagorcular, kurmuştur. Her sayının kendine ait bir karakteri olduğuna inandılar ve bir çok tuhaf geleneği devam ettirdiler.
Pisagorcular, ilk kez bir
“Pisagorcular güneşin doğuşunu kutluyor” Fyodor Bronnikov
Uzaklıkları Hesaplama
Pisagor Teoremi’nin en önemli uygulamalarından biri uzaklıkları hesaplamadır.
Sağda, koordinat düzlemi üzerinde iki nokta görüyorsunuz. Aralarındaki mesafeyi bir cetvel yardımıyla da ölçebilirdik, ama bu tam olarak doğru değil. Bunun yerine, Pisagor Teoremi’ni kullanmayı deneyelim.
Kolayca x-ekseni boyunca uzanan yatay mesafeyi ve y-ekseninde uzanan dik mesafeyi hesaplayabiliriz. Bu iki doğruyu çizersek, dik açılı bir üçgen elde ederiz.
Pisagor’u kullanarak,
Bu yöntem herhangi iki nokta için işe yarar:
Uzaklık Formülü Eğer (
Pisagor Üçlüsü
Önceki adımda
En ünlü örnek 3-4-5 üçgenidir. Çünkü
Eski Mısırlılar Pisagor Teoremi’ni bilmiyordu, fakat 3-4-5 üçgeni hakkında bilgileri vardı. Piramitleri inşa ederken, dik açıyı en iyi şekilde ölçebilmek için uzunlukları 3,4 ve 5 olan düğümlü ipler kullandılar.
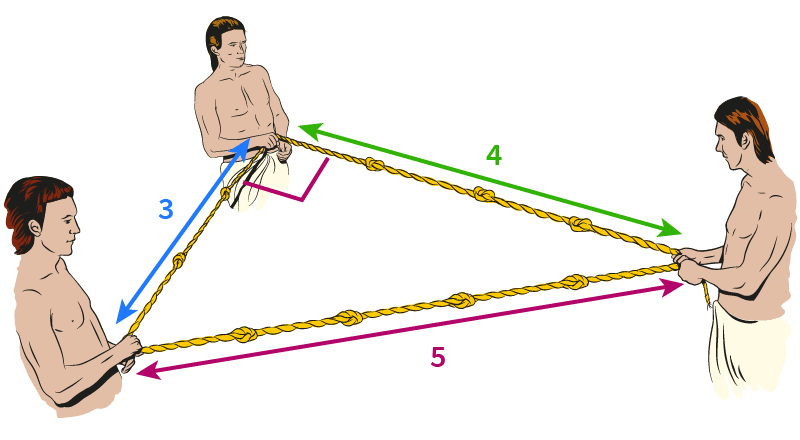
Bu şekildeki üç tam sayı
Bu üçlüleri, koordinat sisteminde karelaj noktaları olarak düşünebiliriz. Geçerli bir Pisagor Üçlüsü için, karelaj noktasından orijine uzaklık bir tam sayı olmalıdır. Aşağıdaki koordinat sistemini kullanarak, Pisagor Üçlülerini bulabilir misiniz?
Bu noktaların dağılmasında herhangi bir yöntem farkettiniz mi?