Vielecke und PolyederPlatonische Körper
Zu Beginn dieses Kurses haben wir
In einem regelmäßigen Polyeder sind alle
Wie sehen also die platonischen Körper aus - und wie viele von ihnen gibt es? Um eine dreidimensionale Form zu erhalten, benötigen wir mindestens

Wenn wir ein Polyeder zusammensetzen, so dass an jeder Ecke drei

Wenn sich an jeder Ecke vier gleichseitige Dreiecke treffen, erhalten wir einen anderen platonischen Körper. Er wird Oktaeder genannt und hat

Wenn sich an jeder Ecke

Wenn

Und sieben oder mehr Dreiecke an jeder Ecke produzieren auch keine neuen Polyeder: Es gibt für so viele Dreiecke nicht genug Platz um eine Ecke herum.
Das bedeutet, dass wir

Wenn

Wenn sich an jeder Ecke
Als nächstes versuchen wir es mit regelmäßigen Fünfecken (Pentagon):

Wenn

Wie zuvor sind vier oder mehr Fünfecke
Das nächste regelmäßige Vieleck, das wir untersuchen wollen ist das Sechseck (Hexagon):

Wenn an jeder Ecke drei Sechsecke zusammentreffen, erhalten wir sofort
Dasselbe gilt auch für alle regelmäßigen Vielecke mit mehr als sechs Seiten. Sie lassen sich nicht zu einer Parkettierung zusammenfügen und man erhält schon gar keine dreidimensionalen Vielecke.
Das bedeutet, dass es nur
Tetraeder
Würfel
Oktaeder
Dodekaeder
Ikosaeder
Beachte, dass die Anzahl der Flächen und Ecken bei Würfeln und Oktaedern sowie bei Dodekaedern und Ikosaedern
Wir können ein Polyeder in sein Dual verwandeln, indem wir jede Fläche durch eine Ecke und jede Ecke durch eine Fläche "ersetzen". Diese Animationen zeigen, wie das abläuft:
Das Tetraeder ist dual mit sich selbst. Da es die gleiche Anzahl von Flächen und Eckpunkten hat, würde das Austauschen nichts ändern.
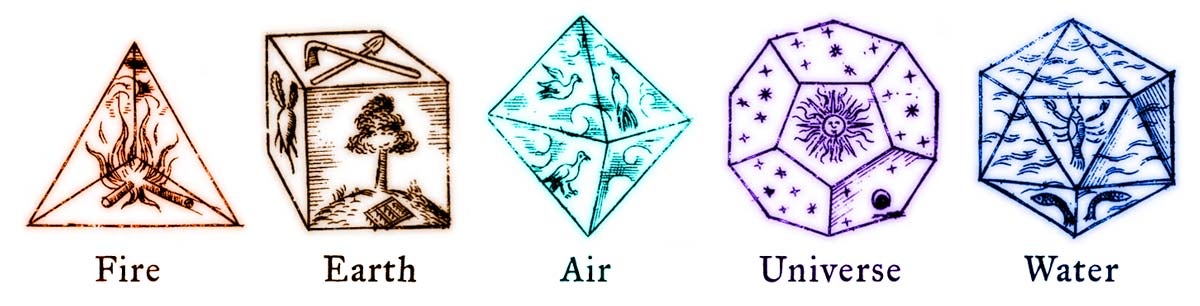
Bilder aus Johannes Keplers Buch "Harmonices Mundi" (1619)
Archimedische Körper
Platonische Körper sind besonders wichtige Polyeder, aber es gibt unzählige andere.
Tetraederstumpf 8 Flächen, 12 Ecken, 18 Kanten
Kuboktaeder 14 Flächen, 12 Ecken, 24 Kanten
Hexaederstumpf 14 Flächen, 24 Ecken, 36 Kanten
Oktaederstumpf 14 Flächen, 24 Ecken, 36 Kanten
Rhombenkuboktaeder 26 Flächen, 24 Ecken, 48 Kanten
Kuboktaederstumpf 26 Flächen, 48 Ecken, 72 Kanten
Abgeschrägtes Hexaeder 38 Flächen, 24 Ecken, 60 Kanten
Ikosidodekaeder 32 Flächen, 30 Ecken, 60 Kanten
Dodekaederstumpf 32 Flächen, 60 Ecken, 90 Kanten
Ikosaederstumpf 32 Flächen, 60 Ecken, 90 Kanten
Rhombenikosidodekaeder 62 Flächen, 60 Ecken, 120 Kanten
Ikosidodekaederstumpf 62 Flächen, 120 Ecken, 180 Kanten
abgeschrägtes Dodekaeder 92 Flächen, 60 Eckpunkte, 150 Kanten
Anwendungen
Platon hatte Unrecht, als er glaubte, dass alle Elemente aus platonischen Körpern bestehen. Aber regelmäßige Polyeder haben viele besondere Eigenschaften, die an anderer Stelle in der Natur zum Vorschein kommen - und wir können diese Eigenschaften in Wissenschaft und Technik kopieren.
Skelett eines Strahlentierchens
Ikosaedrisches Virus
Viele Viren, Bakterien und andere kleine Organismen haben die Form von
Fulleren-Moleküle
Biosphère Montreal
Viele Moleküle sind wie regelmäßige Polyeder geformt. Das bekannteste Beispiel ist
Es wurde 1985 entdeckt, als Wissenschaftler interstellaren Staub erforschten. Sie nannten es "Buckyball" (oder Buckminsterfullerene) nach dem Architekten
Fluorit-Oktaeder
Pyritwürfel
Die meisten Kristalle haben ihre Atome in einem regelmäßigen Gitter angeordnet, das aus
Achteckige Gitterrahmen
Louvre-Museum in Paris
Tetraeder und Oktaeder sind unglaublich steif und stabil, weshalb sie sehr oft für Konstruktionen verwendet werden. Gitterrahmen sind vieleckige Konstruktionen, die große Dächer und schwere Brücken tragen können.
Fußball
Mehrseitige Würfel
Platonische Körper werden auch verwendet, um Würfel zu machen. Aufgrund ihrer Symmetrie hat jede Seite die gleiche
Der