Polygons and PolyhedraPlatonic Solids
At the beginning of this course we defined
In a regular polyhedron all
So what do the Platonic solids look like – and how many of them are there? To make a three-dimensional shape, we need at least

If we create a polyhedron where three

If four equilateral triangles meet at every vertex, we get a different Platonic solid. It is called the Octahedron and has

If

If

And seven or more triangles at every vertex also don’t produce new polyhedra: there is not enough space around a vertex, to fit that many triangles.
This means we’ve found

If

If
Next, let’s try regular pentagons:

If

Like before, four or more pentagons
The next regular polygon to try are hexagons:

If three hexagons meet at every vertex, we immediately get a
The same also happens for all regular polygons with more than six sides. They don’t tessellate, and we certainly don’t get any three-dimensional polygons.
This means that there are just
Tetrahedron
Cube
Octahedron
Dodecahedron
20 Vertices
30 Edges
Icosahedron
12 Vertices
30 Edges
Notice how the number of faces and vertices are
We can turn a polyhedron into its dual, by “replacing” every face with a vertex, and every vertex with a face. These animations show how:
The tetrahedron is dual with itself. Since it has the same number of faces and vertices, swapping them wouldn’t change anything.
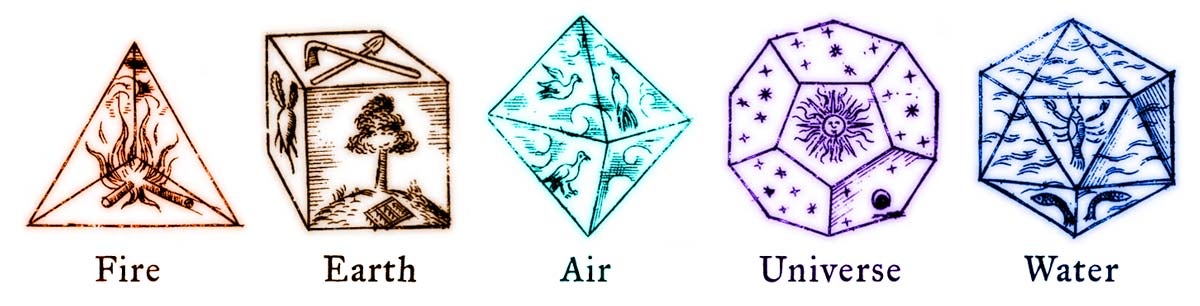
Images from Johannes Kepler’s book “Harmonices Mundi” (1619)
Archimedean Solids
Platonic solids are particularly important polyhedra, but there are countless others.
Truncated Tetrahedron
8 faces, 12 vertices, 18 edges
Cuboctahedron
14 faces, 12 vertices, 24 edges
Truncated Cube
14 faces, 24 vertices, 36 edges
Truncated Octahedron
14 faces, 24 vertices, 36 edges
Rhombicuboctahedron
26 faces, 24 vertices, 48 edges
Truncated Cuboctahedron
26 faces, 48 vertices, 72 edges
Snub Cube
38 faces, 24 vertices, 60 edges
Icosidodecahedron
32 faces, 30 vertices, 60 edges
Truncated Dodecahedron
32 faces, 60 vertices, 90 edges
Truncated Icosahedron
32 faces, 60 vertices, 90 edges
Rhombicosidodecahedron
62 faces, 60 vertices, 120 edges
Truncated Icosidodecahedron
62 faces, 120 vertices, 180 edges
Snub Dodecahedron
92 faces, 60 vertices, 150 edges
Applications
Plato was wrong in believing that all elements consists of Platonic solids. But regular polyhedra have many special properties that make them appear elsewhere in nature – and we can copy these properties in science and engineering.
Radiolaria skeleton
Icosahedral virus
Many viruses, bacteria and other small organisms are shaped like
Buckyball molecule
Montreal Biosphere
Many molecules are shaped like regular polyhedra. The most famous example is
It was discovered in 1985 when scientists researched interstellar dust. They named it “Buckyball” (or Buckminsterfullerene) after the architect
Fluorite octahedron
Pyrite cube
Most crystals have their atoms arranged in a regular grid consisting of
Octagonal space frames
Louvre museum in Paris
Tetrahedra and octahedra are incredibly rigid and stable, which makes them very useful in construction. Space frames are polygonal structures that can support large roofs and heavy bridges.
Football
Polygonal role-playing dice
Platonic solids are also used to create dice. because of their symmetry, every side has the
The