Divisibility and PrimesThe Distribution of Primes
The easiest way to check if a number is prime is to try to divide it by all smaller integers. Computers can do this very quickly and efficiently. For very large numbers, with hundreds of digits, there are also more efficient algorithms. Some of these even use probability to determine if a number is almost certainly prime.
Here is a calculator that allows you to check if any number is prime:
Prime Checker
Throughout history, people have tried to find larger and larger prime numbers. In 1460, the largest known prime was 131,071. In 1772,
With the arrival of computers in the 20th century, calculating large primes became much easier. The largest currently known prime was discovered in December 2018 and has 24,862,048 digits. You would need 8000 sheets of paper to print it out!

GIMPS (Great Internet Mersenne Prime Search) is a collaborative project, where volunteers can find primes using free software.
Calculating these large prime numbers might seem like just a waste of time, but later in this course you’ll learn about various real life applications where computers have to use large primes.
Here you can generate your own prime numbers with a given number of digits:
Prime Generator
Number of digits:
The Ulam Spiral
The Polish mathematician
We write down all integers in a rectangular grid, starting with 1 in the middle and then spiralling outwards. Then we highlight all numbers which are prime.
So far, the Ulam spiral doesn’t look particularly exciting. But if we zoom out, interesting patterns emerge. Here are the primes up to 160,000:
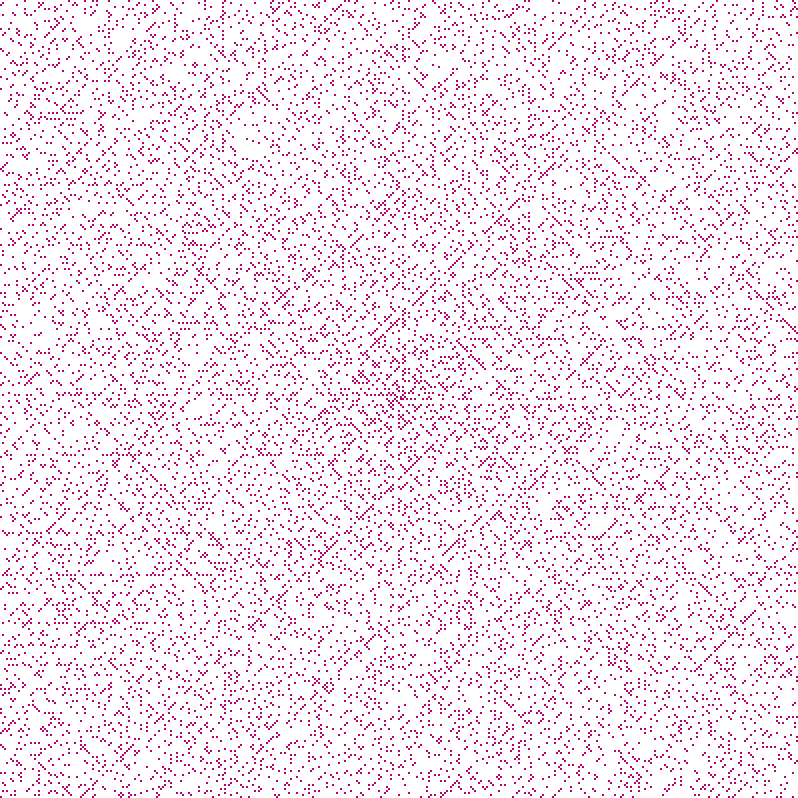
Rather than appearing randomly, as one might expect, it seems that certain diagonals are much more popular with primes than others. This creates a curious “plaid” pattern.
It turns out that these diagonals all correspond to certain quadratic equations which seem to generate prime numbers more often than average. However it is unknown why that would be the case…
Cover of the March 1964 issue of Scientific American
The Goldbach Conjecture
In 1742, the German mathematician
Goldbach Calculator
Pick any even number, to calculate how it
can be written as the sum of two primes.
Goldbach wrote about his observation in a letter to the famous mathematician
Computers have checked that the Goldbach Conjecture works for every even number up to 4 × 1018 (that’s a 4 with 18 zeros), but mathematicians have still not found a proof that it works for all even integers. And that is a big difference, because there are infinitely many integers, so we couldn’t possibly check all of them.
Its apparent simplicity made the Goldbach conjecture one of the most famous unsolved problems in mathematics.
Twin Primes
We have already seen that prime numbers get more spread out as they get bigger. But they always seem to appear completely random, and occasionally we find two primes right next to each other, just one number apart: these are called Twin Primes.
35,1113,4143,101103,20272029,108,377108,379,1,523,6511,523,653
The largest known pair of twin primes has an incredible 58,711 digits! But are there infinitely many twin primes, just like there are infinitely many primes? Nobody knows – the Twin Prime conjecture is another one of the many unsolved problems surrounding the primes.
The Riemann Hypothesis
Mathematicians have spent many centuries exploring the pattern and distribution of prime numbers. They seem to appear completely randomly – sometimes there are huge gaps in between consecutive primes, and sometimes we find
When only 15 years old, the German mathematician
Along the x-axis you can see all integers. Whenever there is a prime, the Prime Counting Function (shown in blue) increases by one. As we
However, as you can see above, there is still a significant error between the actual number of primes, and Gauss’s approximation. In 1859, the mathematician
Hundreds of mathematicians have tried to prove Riemann’s hypothesis, but all without success. It is often considered one of the most difficult and most important unsolved problems in mathematics. In 2000, the Clay Mathematics Institute named it one of seven